高数中的第一个证明,可能就是这个$\lim\limits_{x\rightarrow 0} \frac{\sin x}{x} = 1$的证明了。下面给出这个极限的证明,用到了解析几何(作图法)。
作图工具 Geometry
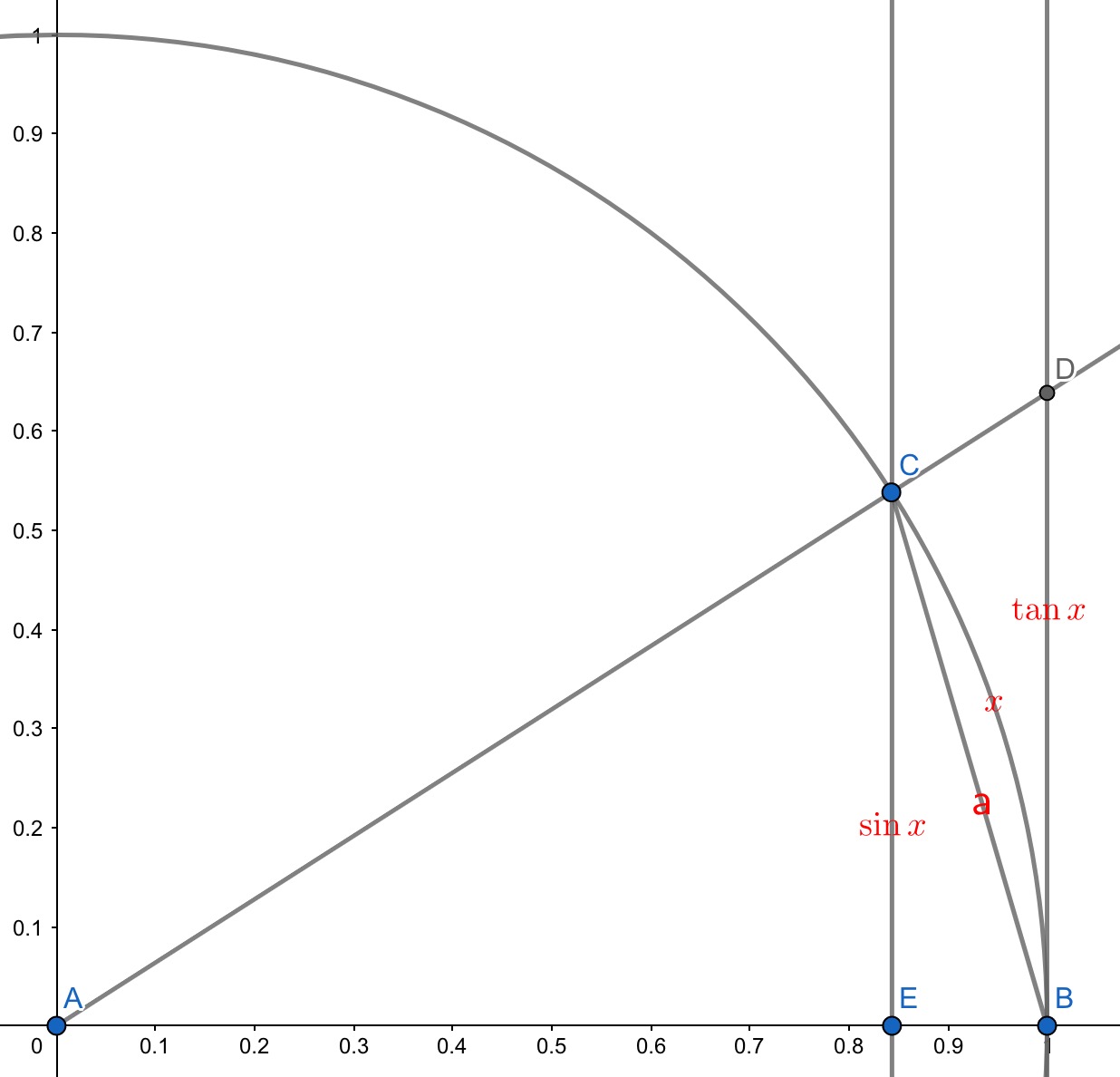
如图我们可以看到,有一个单位圆,圆心为 $A$ ,线段 $CE$ 的长度等于 $\sin x$,线段 $CB$ 是 弦(我们令他等于 $a$),弧 $\overset{\frown} {CB}$ 的长度就是 $x$,线段 DB 的长度等于 $\tan x$。
它们的长度的大小关系我们很容易得出:
- $\sin x < a$,因为三角形的直角边小于斜边
- $a < x$,因为两点之间线段最短
- $x < \tan x$,这个略微不那么直接,可以用面积法(通过比较面积继而得到表达式中两个未知数的大小关系),扇形 $CAB$ 的面积:$\frac{1}{2} \cdot 1 \cdot x$ ,三角形 $\triangle DAB$ 的面积:$\frac{1}{2} \cdot 1 \cdot \tan x$ 。而 $CAB$ 的面积小于 $DAB$ 的面积。所以得到 $x < \tan x$
由此我们得到不等式:$\sin x < x < \tan x$ (当 $x>0$ ),同时除以 $\sin x$,得到:$1 < \frac{x}{\sin x} < \frac{1}{\cos x}$。
当 $x<0$ 时,显然 $\sin x > x > \tan x$,同时除以 $\sin x$(除以负数要变号),得到:$1 < \frac{x}{\sin x} < \frac{1}{\cos x}$。
令 $x\rightarrow 0^{-}$,由夹逼定理得到左极限 $\lim\limits_{x\rightarrow 0^{-}} \frac{\sin x}{x} = 1$
令 $x\rightarrow 0^{+}$,由夹逼定理得到右极限 $\lim\limits_{x\rightarrow 0^{+}} \frac{\sin x}{x} = 1$
最终可以得到:$\lim\limits_{x\rightarrow 0} \frac{\sin x}{x} = 1$ (左右极限都等于 1)