今天看到下面这个公式,突然想我好像不会推导啊:
$\sin(\beta-\alpha) = \sin\beta\cos\alpha - \cos\beta\sin\alpha$
遂想如何推导,在 youtube 上找了一个视频:三角函数正余弦和角公式推导
思路是先推导出:$\cos(\beta-\alpha) = \cos\alpha\cos\beta + \sin\alpha\sin\beta$
然后根据这个再结合正弦余弦之间的关系就很容易推 $\sin(\beta-\alpha) = \sin\beta\cos\alpha - \cos\beta\sin\alpha$
那么怎么推导上面这个公式呢?
需要用到解析几何:
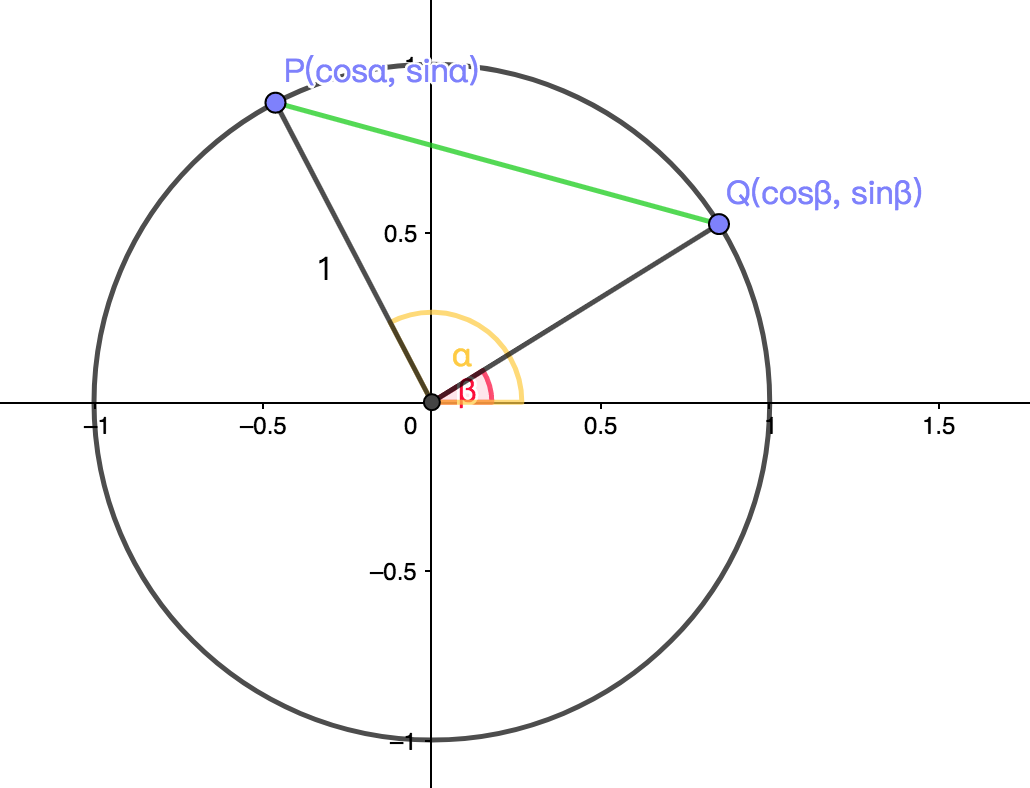
结合 勾股定理 和 余弦定理 可以推导出。
这里不给出勾股定理和余弦定理的证明,感兴趣的可以自己证。
根据勾股定理:
$$
\begin{align}
\overline{PQ}^2
&= (\sin\alpha - \sin\beta)^2 + (\cos\beta - \cos\alpha)^2 \newline
&= 2 - 2(\cos\alpha\cos\beta + \sin\alpha\sin\beta) \newline
\end{align}
$$
根据余弦定理($a^2 = b^2 + c^2 -2ab\cos A$):
$$
\begin{align}
\overline{PQ}^2
& = 1^2 + 1^2 - 2\cdot1\cdot1\cdot\cos(\alpha-\beta)
\end{align}
$$
由此推出:
$$
\cos(\alpha-\beta) = \sin\alpha\sin\beta+\cos\alpha\cos\beta
$$
也即:
$$
\cos(\beta-\alpha) = \sin\alpha\sin\beta+\cos\alpha\cos\beta
$$
然后:
$$
\begin{align}
\sin(\beta-\alpha)
&= \cos(\frac{\pi}{2}-(\beta-\alpha)) \newline
&= \cos((\frac{\pi}{2}+\alpha) - \beta) \newline
&= \sin(\frac{\pi}{2}+\alpha)\sin\beta + \cos(\frac{\pi}{2}+\alpha)\cos\beta \newline
&= \cos\alpha\sin\beta - \sin\alpha\cos\beta \newline
&= \sin\beta\cos\alpha - \cos\beta\sin\alpha
\end{align}
$$